海伦-秦九韶公式的证明

海伦-秦九韶公式是一个非常有趣的公式，可以通过三角形的三条边求出三角形的面积，在我学的初中课本中虽然有提到但没有证明方法。现在我就写一下我初中写的证明方法

构造图形

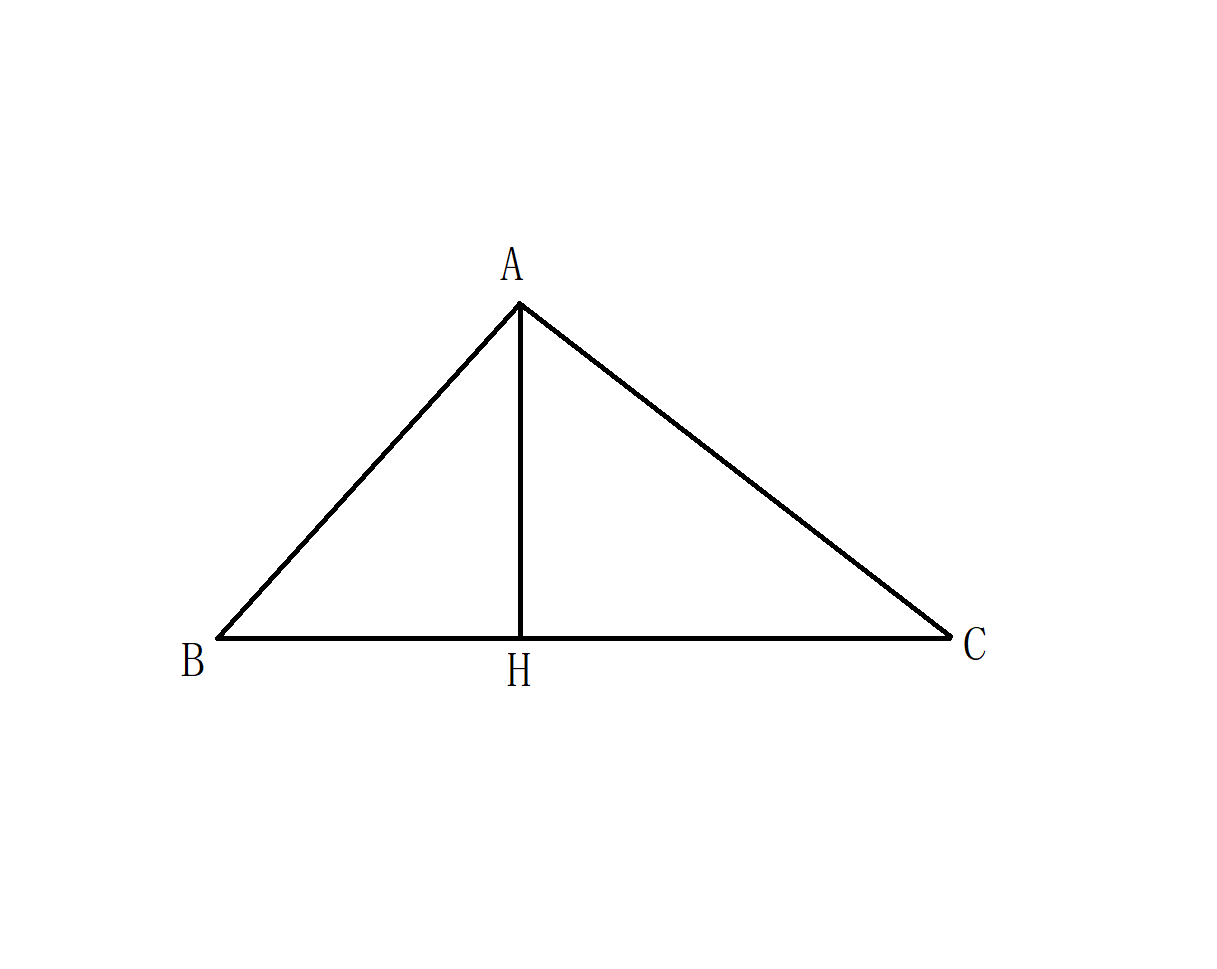
首先，我们需要画一个三角形ABC，设A点的对边是a，B点的对边是b，C点的对边是c

证明余弦定理

过A作AH⊥BC于H,设BH为d

因为 BC=a,BH=d

所以 CH=BC-BH=a-d

因为 =+

所以 =-=-,

因为 ==-2ad+

所以 ==+=-+-2ad+=+-2ad

因为 AH⊥BC

所以 ∠AHB = 90°

所以 cosB =

所以 d = BH = AB cosB = c cosB

所以 =+-2ad=+-2ac*cosB

所以 =+-2ac*cosB

证明海伦-秦九韶公式

因为余弦定理可知在三角形ABC中已知abc可求cosB

即 cosB =

又因为 +=1

所以 =1-

所以 =
=-
=
=
=
=
=

所以 AH=

所以 三角形ABC的面积=
=
=
=
=
=

设 p=

所以 三角形ABC的面积=