定义无穷大——无穷大的一种理解方法

需要注意的是这个理论目前还不算成熟，只算是无穷的另一种理解方式

奇妙的对应

实数集有一个非常奇妙的性质，那就是实数集中没有一个最大的数，也没有一个最小的数

还有一种集合也有这种性质，那就是开区间，如(-1, 1).

而我们知道(-1, 1)与实数集有相同的势———阿列夫1.

也就是说实数集与开区间(-1, 1)至少存在一种一一对应关系

那么我们就可以把正实数与(0, 1)中的数一一对应，(-1, 0)与负实数一一对应。而0对应0.

那么我们就可以把正无穷这个大于一切实数的非实数对应成1，负无穷这个非实数对应成-1

这就是这个理论的精髓，把无穷大定义成与实数集连续的数，且把无穷大映射到有穷的范围内。

至于对应关系则非常好找。例如：

(x > 0) 时 ：f(x) = 1 -

(x = 0)时 ：f(x) = 0

(x < 0) 时 ：f(x) = - 1

这个函数的图像如下图所示

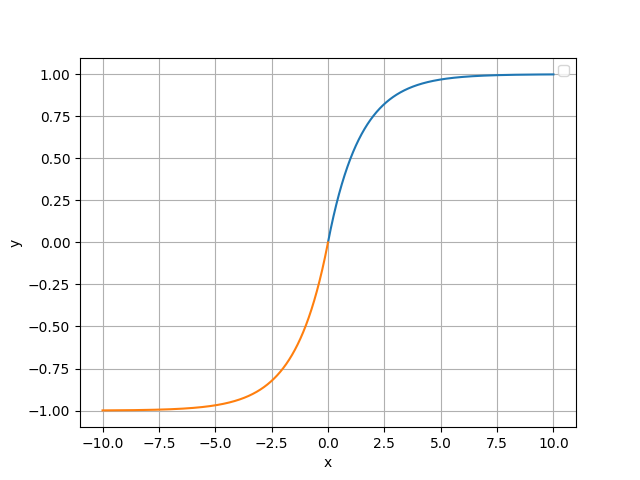
这时我们就可以把实数集这个无穷区间映射到（-1， 1）这个有穷区间

例子

下面我就那这套理论证明一下正无穷加一仍等于正无穷

首先我们定义一个正常xoy坐标系,再建立一个小坐标系mon。m,n的取值范围为[-1, 1]

那么坐标系xoy中第一象限的函数图像向坐标系mon中映射的规则即为

m = 1 -

n = 1 -

那么对于y = x + 1就可以得出

m = 1 -

n = 1 -

= 1-m

= (1-m)/2

1 - = 1 - (1-m)/2

n = 1 - (1-m)/2

当m = 1时n等于1

QED