一种侧面展开图求法

题目：
一个圆柱，按如图所示的方式切割，下半部分几合体的侧面展开图是什么？

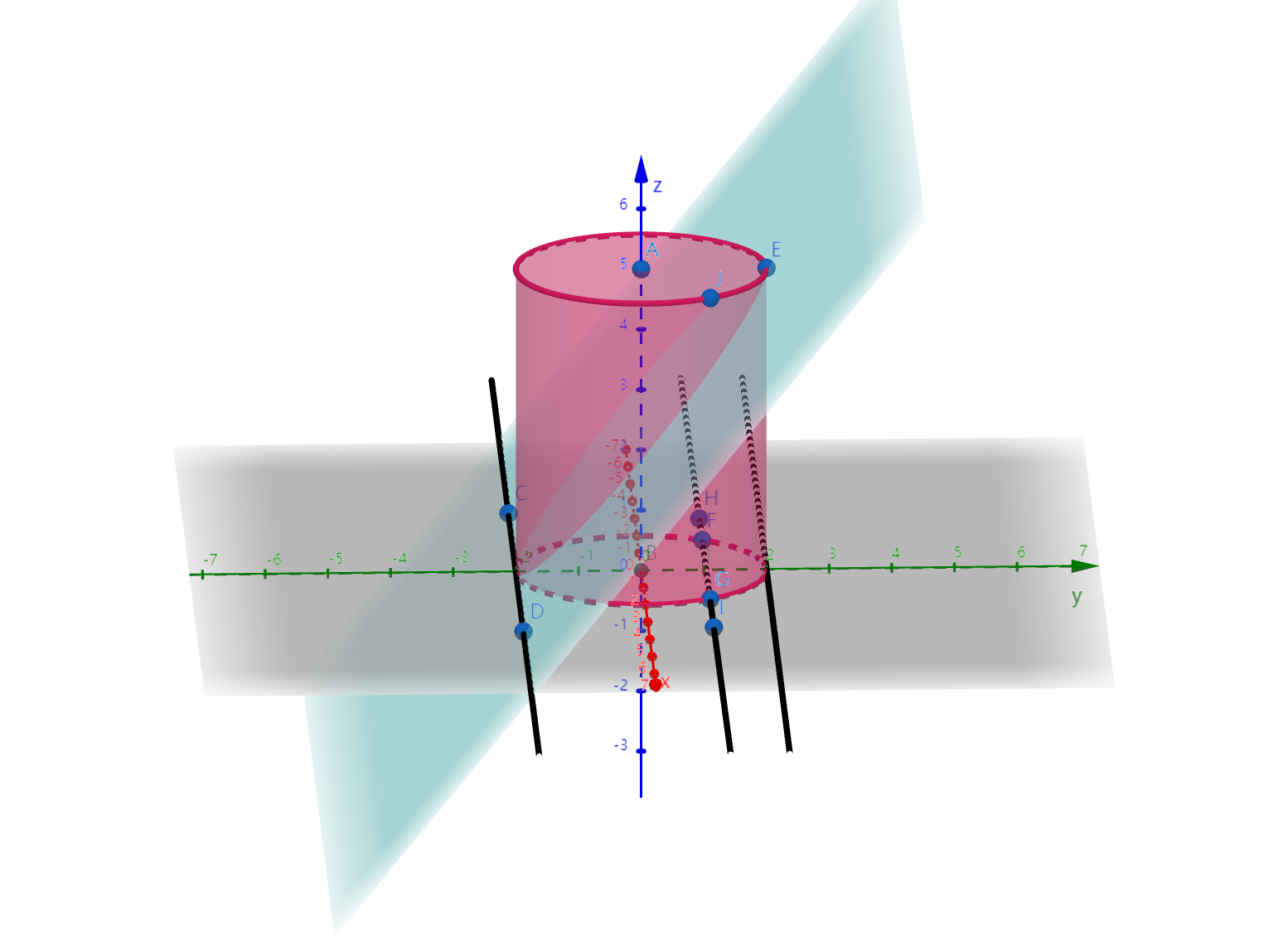
前期准备

首先建立如图所示的坐标系

接着，建立一个垂直与圆柱底面的平面，且与底面的交线与y轴垂直。
并使之从左往右扫过

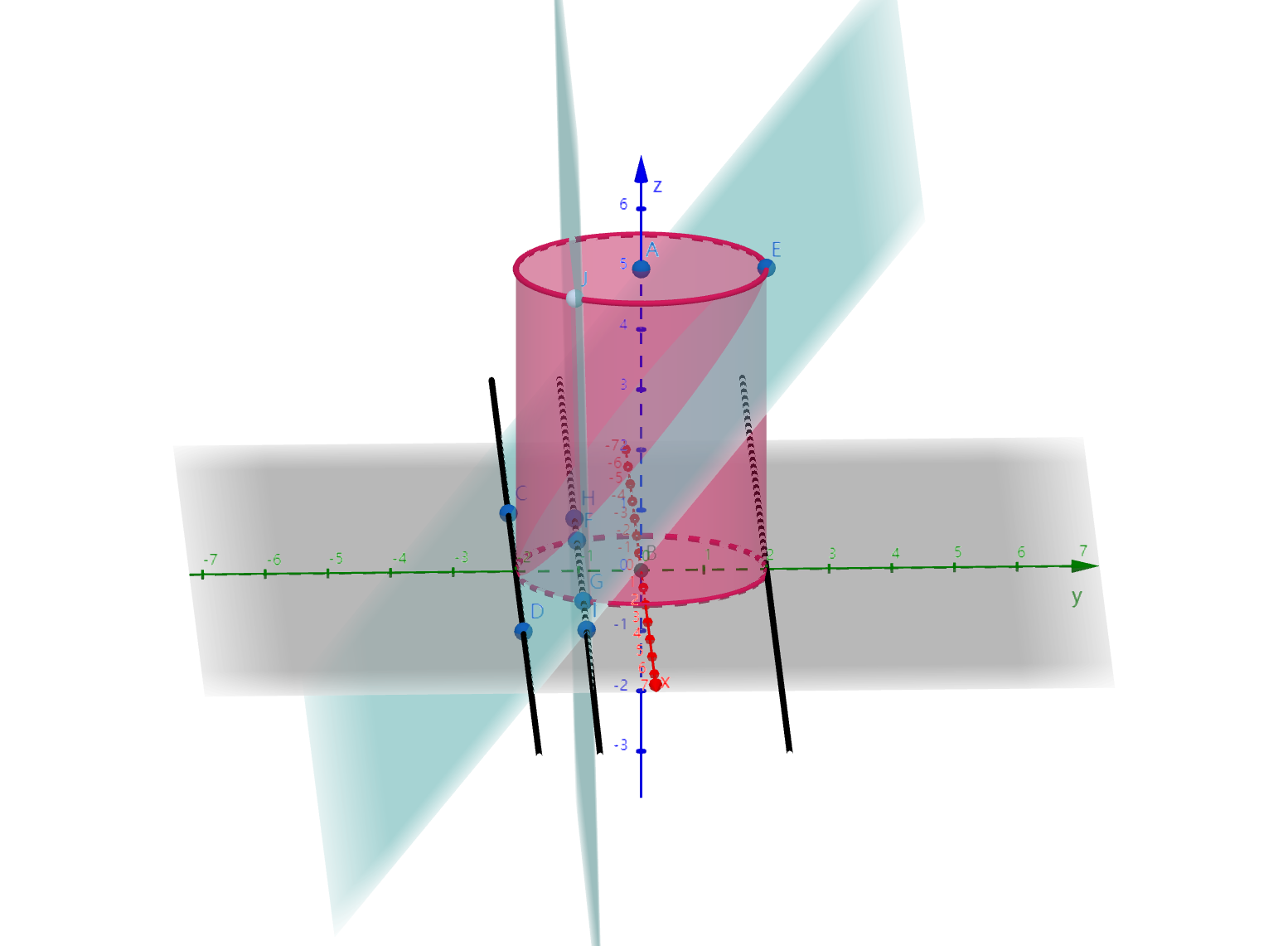
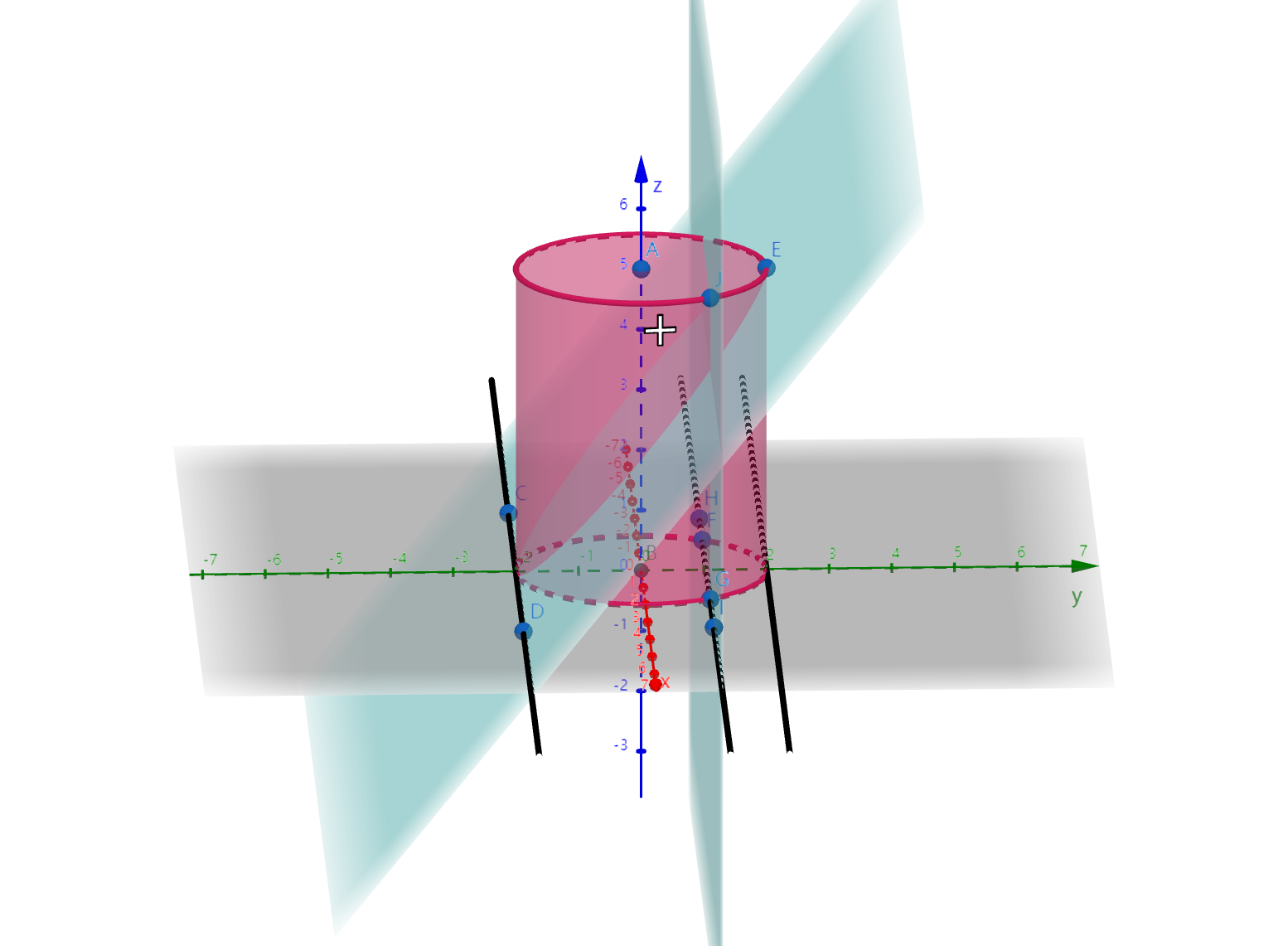
分析

1.定性分析

(1)关注侧面
平面在从左往右匀速扫的过程中，随着y轴上数值的匀速增加，平面与截面交点在z轴上的数值匀速增加。（下文无特殊说明一律用z轴上的数值代指所作平面与截面交点在z轴上的数值，下文无特殊说明一律用y轴上数值代指所作平面与y轴交点在y轴上的数值 ）

(2)关注底面
设竖直平面与底面圆的交点中处在x轴非负半轴的交点为P。
平面在从左往右匀速扫的过程中，随着y轴上数值的匀速增加，P点移动的速度先快后慢再快，且易得在如图所示的位置速度最慢。

(3)得出侧面展开图图像

因为平面在从左往右匀速扫的过程中，随着y轴上数值的匀速增加，P点移动的速度先快后慢再快

所以若P点匀速移动，则y轴上的数值先慢后快再慢。

因为随着y轴上数值的匀速增加，z轴上的数值匀速增加。

所以若P点匀速移动，则z轴上的数值先慢后快再慢，对应图像的斜率起初很小，然后逐渐变大，最后逐渐变小。

而P点移动的路程即为侧面展开图的横轴，z轴上的数值即为侧面展开图的纵轴。

所以可得出如下图图像

由对称性可知，P点运动到另一半圆时的侧面展开图图像与前一半对称，可得出完整图像

2.定量分析

建立一个平面直角坐标系并作出圆柱底面圆（假设半径为1）

设OP连线与横轴非负半轴所呈的最小正角为α,P点移动的路程为x,z轴上的数值为y

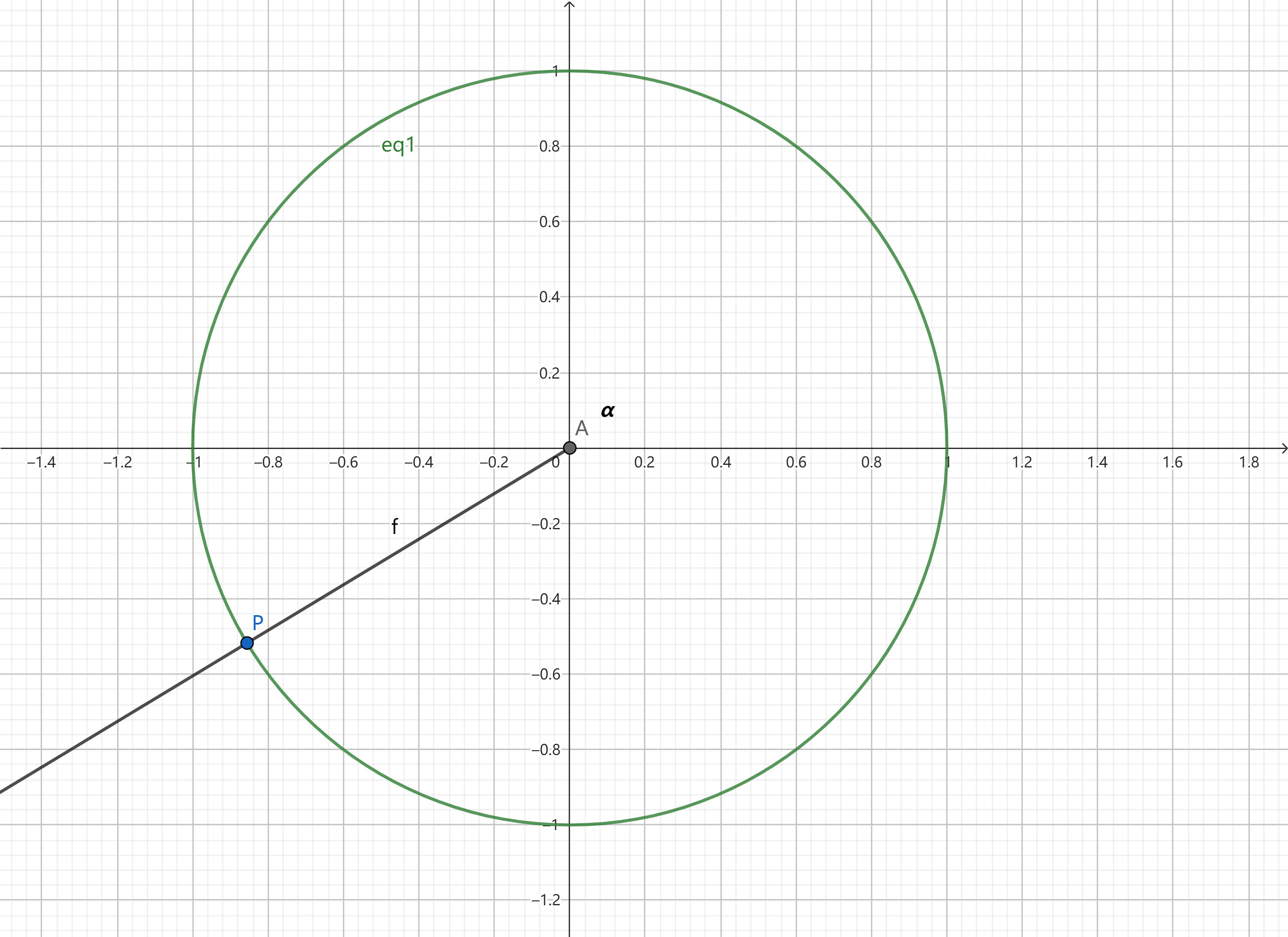
易得出

x = α - π

y = k * cos(α) + b

所以 y = k * cos(x + π) + b

所以y = -k * cos(x) + b

由题意可知，图线过(0, 0), (π, h) 两点，得 k = b = h / 2

这里假设h = 6

即可得出如下图图像

完结