关于竖直平面内圆周运动最小速度的一些证明

我们都知道，在竖直平面内只有外侧轨道的圆周运动中，忽略阻力后，在圆周运动的最高点最小速度是

这个结论是怎么得出的呢，其实就是让最高点仅由重力提供向心力，即

那么这样得出的结论真的万无一失吗？

上述过程只证明了它如果可以运动到最高点，那么它刚好可以通过最高点。但它真的可以运动到最高点吗？这其实不然。

问题简化

首先，由机械能守恒可知，在运行到同一高度时，它的速度相同，那么我们就可以只考虑右半轨道

然后，易得在右下90°时，小球一定不会离开轨道，所以，我们就只需考虑右上90°轨道

开始证明

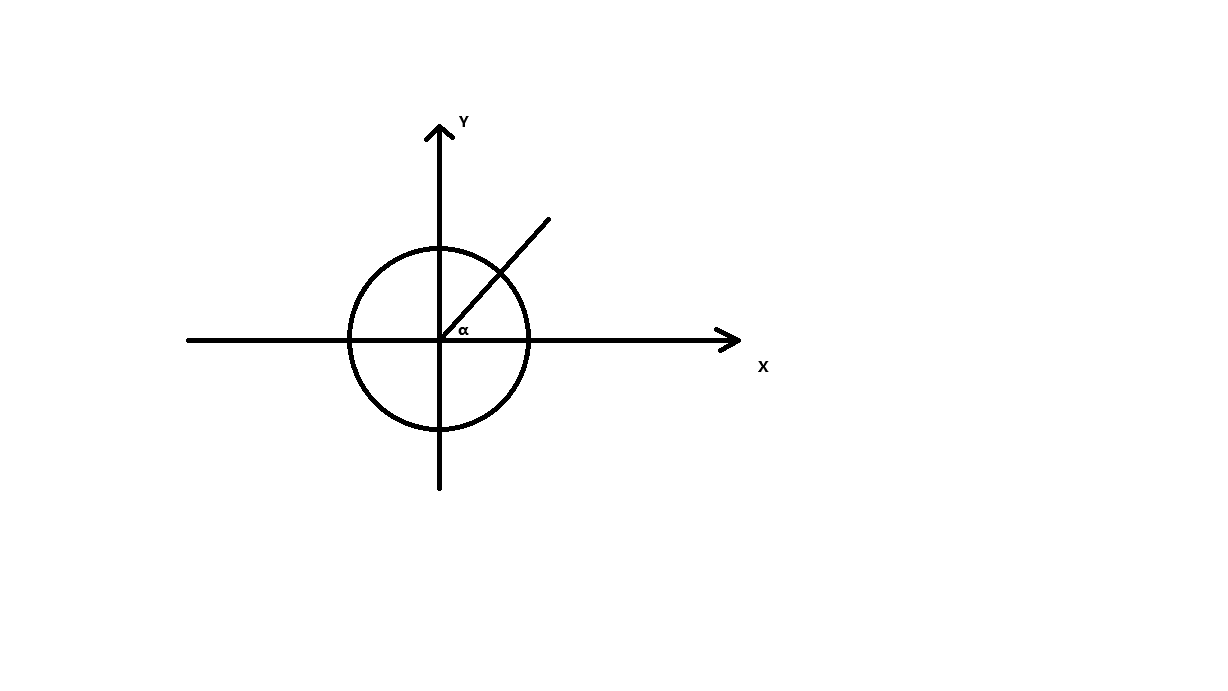
由机械能守恒得 最高点时

当角度为α时 h = Rsin(α)

此时,由机械能守恒得

支持力为F

因为 0° <= α <= 90°

所以 F>=0

证毕