等量同种电荷所成电场在电荷连线中垂线上的最大值点问题与重根法的原理及应用
高中物理在学习库仑定律时有这样一个规律,等量同种电荷所成电场在电荷连线中垂线上存在两个电场强度最大值点,在这两个最值点两次电场强度递减,在连线中点和中垂线无穷远处最小。
建立模型
首先我们可以建立如下模型:
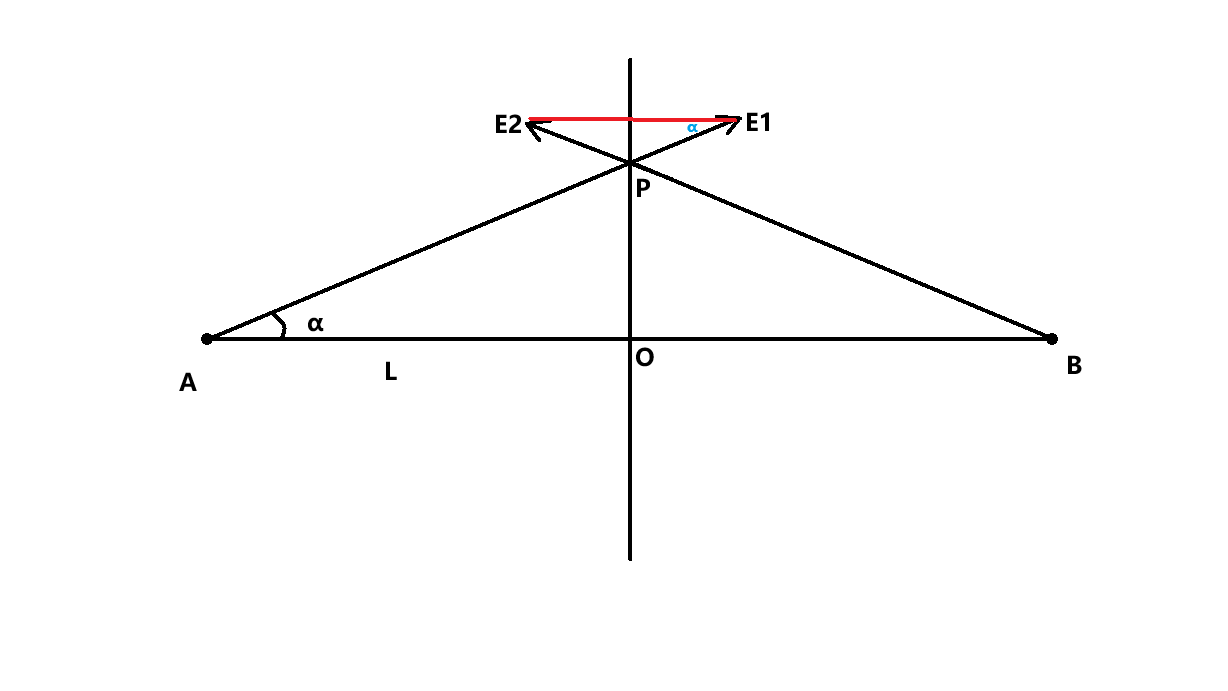
A,B为等量同种电荷且电荷量设为q
PO 为 AB 中垂线
L 为 AO 线段长
P 为中垂线上任意一点
α 为∠PAO
那么,有库伦定律及电场强度计算公式可知
根据E1, E2的位置关系可知
对于求最值来说,它的常数部分可以忽略,所以我们只需关注变量部分即
再进行一个简单的换元得到
而下半部分可以用对称性简单得到
数学part
下面让我隆重介绍重根法
首先我们可以想见,这个函数会是一个单峰函数,那么如果做一条水平线就会有如下特点:
1.在最大值处,有且仅有一个交点
2.在最大值两处,或没有交点,或有两个不同交点
3.水平线越接近最值点纵坐标,两交点越接近最值点横坐标
所以设这两个交点的横坐标为a, b
由它们的纵坐标相等可得
移项得
因式分解得
由 a - b ≠ 0 可知
而由于某种神奇的原因(下一部分讨论),我们可以代入 a = b,即两个交点重合为一个交点
这时
所以最大值点出现在sinα =
重根法原理
以本题为例,我们得到的关系式